PretensT
Tensegrity is a special kind of structure made of push and pull.
Project maintained by elastic-interval Hosted on GitHub Pages — Theme by mattgraham
Elastic Interval Geometry
Sometimes it’s good to start from scratch. One advantage is that it becomes easier to understand because nothing is hidden.
The pretenst app has an impressive realism to it, but making this work properly is remarkably uncomplicated. The core is a single simple idea: the Elastic Interval which is a thing which holds on to two points in 3D space.
Because it exists in time, the best way to think about an interval is to imagine it to be a tiny robot which sleeps most of the time, but periodically wakes up for a moment to push or pull on its two points. This robot doesn’t know about anything but its two points.
(☆)↔↔↔↔😎↔↔↔↔(☆)
too long
((☆→→→→→😠←←←←←☆))
too short
☆))←←←😠→→→((☆
We call the points “joints” because there is one more very important element to the Elastic Interval model. The robots share joints, which means that the robots can affect each other, despite that they don’t know about each other.
↔ (☆) ↔
↕
Together these intervals and joints define a whole 3D geometry which exists in time. It’s surprising to see what can come from such a simple foundation.
Time
We need all of the pushing and pulling done by all of the tiny robots to be fair.
If only some of the intervals were to be activated at one time, the joint may jerk suddenly in one direction. Later, the other intervals may be activated, causing the joint to jerk again in the other direction.
A jerky model would not be very authentic so, the model of time that we will use will operate in a sweeping fashon, where every element gets an opportunity to activate during the same moment.
In other words all parts if the entire model, however many intervals and joints, will experience an entire moment simultaneously and be finished with it before the next moment. The moments effectively sweep through the whole model, exactly the way it happens in cellular automata.
This kind of time is more the way we thought about it before Einstein wrapped it up together with space and everything got weird. One day we might go there (note the interval has its name to keep the door open for “time interval”) but for now, we’ll stick with Newton’s time.
Split Moments
The dance performed by these joints and intervals is animated by splitting a moment in two: first sweeping through the intervals, and then through the joints. During each moment, the intervals will each express their discomfort and the joints will each strive to find the best compromise.
- intervals push and pull
- joints move
- intervals push and pull
- joints move
- intervals push and pull
- …
A joint knows where it is in space, but an interval doesn’t. An interval only knows about the two joints that it touches, and whether they are too close to each other or too far apart. An interval is not aware of the fact that the world has three space dimensions, since it lives in its own one-dimensional world.
During an interval sweep, every interval is activated in turn, which means that it has an opportunity to express itself. If the interval’s two joints are too close it will ask the joints to move away, and if they’re too far it will ask them to get more together.
When the interval sweep is finished, all intervals have expressed themselves, and the model is ready for the joint sweep. Joints have been accumulating requests from the various interval ends touching them, but a joint interprets each request differently since it knows about three dimensions. The joint interprets the one-dimensional requests by combining them with the direction of each interval, turning them into direction requests.
A joint’s job is to mediate between the different intervals and try to satisfy them as well as it can, so it weighs all of the direction requests to decide where to jump. The new position in space should be the best compromise between the needs of the intervals.
When all joints have jumped, the moment is finished and the model begins the next moment. Once again the intervals will express their discomfort and the joints will strive to find the best compromise.
Tetrahedron
The simplest 3D thing that occupies some space and can be built using elastic intervals and joints is the tetrahedron using four joints and six intervals.
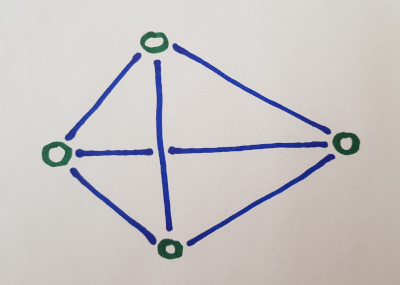
This of course means a tetrahedron in time, so if it gets squeezed in some direction its intervals would push or pull to regain the original shape.
Separate Push and Pull
What if some intervals only ever push while others only ever pull?
It turns out that a stable tetrahedron can no longer be built because it will inevitably collapse when some intervals cannot push. A tetrahedron needs its intervals to both push and pull to maintain its volume. If we want to have volume but we only have pushes and pulls to work with, we need some more parts.
The simplest thing you can make now is actually a tensegrity structure where the pushing intervals don’t touch each other which we call the twist.
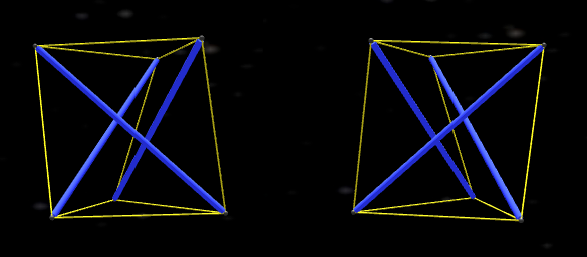
At a minimum we need three pushes and nine pulls.
Unlike the tetrahedron, the twist has an orientation, so is either a left twist or a right twist.
Coming up next
Next we will look at how to build much more complicated structures made of many intervals and joints.
To do that, we will need a language to describe the building process.
Projects:
2024-07-23: "Bouncy Wooden Sphere": what you can do with a discarded bed2024-04-23: "Twisted Torque": tied into a permanent twist
2023-03-27: "Easy 30-Push Sphere": one simple element
2022-10-05: "Glass and LED": going big and colorful
2022-09-29: "Fascia": dancing with tensegrity
2022-08-30: "Mitosis": the four-three-two tensegrity
2022-08-04: "Push Bolts for the People": finalizing design and getting it out there
2022-06-22: "Head to Head Push Bolt": M5 and M6 bolts symbiosis
2022-05-30: "Hiding Knots": bump up the aesthetics
2022-05-25: "Innovation with 3D Printer": the push bolt
2021-12-02: "Headless Hug": breaking a rule for the sake of symmetry
2021-10-28: "Rebuilding the Halo": finally got it right
2021-10-20: "Convergence": growing and reconnecting
2021-07-27: "120-Strut Brass Bubble": taking the next step up in complexity
2021-05-26: "30-Strut Brass Bubble": bouncing spherical tensegrity
2021-04-08: "Bow Tie Tensegrity": better bend resistance
2021-03-29: "Six Twist Essential": what if more hands could see?!
2021-01-25: "Minimal Tensegrity": no more tension lines than absolutely necessary
2021-01-18: "Degrees of Freedom": first adjustable hybrid tensegrity
2021-01-11: "Fractal Experiment": a tensegrity of tensegrities
2020-12-09: "Axial Tension": pretensing what is already pretenst
2020-11-02: "Halo by Crane - Part 2": the strengthening
2020-10-26: "Halo by Crane - Part 1": assembly complete but strength lacking
2020-10-12: "Brass and Tulips": a tight and strong tensegrity tower
2020-08-10: "Prefab Tension Tower": the tower of eight twists
2020-07-27: "Elastic Bubble": building with elastic ease
2020-07-13: "The Twist Sisters": left-handed and right-handed
2020-07-06: "Radial Tension": Pulling towards the middle
2020-06-22: "Diamond of Tension": Four pulls for every push
2020-06-15: "Prefab Tension": Separating compression from tension